스탠포드의 CS229: Machine Learning 강의를 듣고 정리하는 포스팅입니다.
Linear Regression
Linear Regression이란 선형회귀라고 번역된다. Linear Regression 알고리즘은 선형 함수로 풀 수 있는 회귀 문제에 적용된다.
집 값 예측 문제를 예시로 들 수 있다.
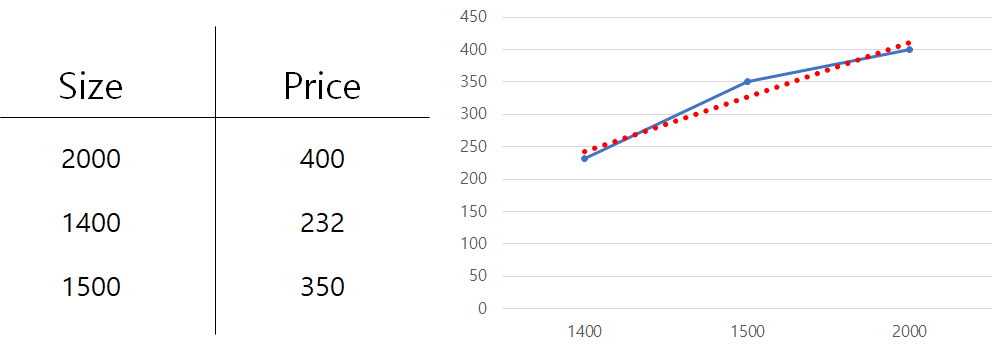
예시로 집의 면적과 가격에 대한 데이터를 왼쪽 표로 나타내고, 오른쪽에는 차트로 나타내었다.
차트의 X축은 Size, Y축은 Price이다.
차트에서 파란색 선이 실제 데이터의 값을 이은 선이고, 빨간색 선이 데이터의 추세를 표시한 추세선이다.
Linear Regression은 이렇게 y값이 연속적인 문제에서 선형 함수를 사용하여 새로운 데이터 X가 들어왔을 때 Y를 예측하는 문제를 푸는 알고리즘이라고 할 수 있다.
이 문제를 푸는 순서는 다음과 같이 정리할 수 있다.

먼저 실제 데이터들이 많이 있는 Training Set을 준비하고, 학습하고, 가설 H를 만든다.
그 뒤에 새로운 데이터 x를 가설 H에 대입하여 x에 대한 y값을 예측한다.
여기서 가설은 다음과 같은 식이다.
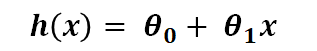
가설이란 새로운 데이터 x가 들어왔을 때 y를 예측할 수 있는 식이라고 생각하면 된다.
모델은 파라미터인 theta (θ)를 계속해서 업데이트하면서 학습한다.
위 식에서 x는 feature의 개수이다.
feature가 많아지면 아래의 식과같이 표현된다.
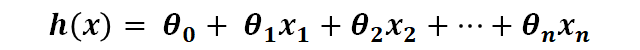
이 식의 표기법을 단순화한 식은 아래와 같다. (n은 feature의 개수)

표기법 정리
앞으로 강의에서 사용될 표기법에 대해서 정리한다.
이 표기법은 강의에서만 사용되는게 아니라, 보편적으로 표현되는 기호이므로 알아두면 좋다.

How to choose parameter(theta)?
이제 가설 h(x)를 배웠으니, h(x)가 y에 가장 가까운 예측을 하도록 해야한다.
즉, h(x)가 y에 가깝도록 θ를 잘 골라야한다. 어떻게 잘 고를 수 있을까?
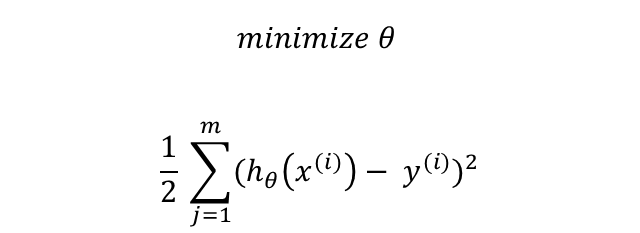
모델의 예측값과 실제 y값의 차이를 제곱한 것이다.
우리는 앞으로 이 식을 J(θ) 혹은 비용함수라고 부를 것이다.
여기서 θ를 최소화하기 위해 이 식을 사용한다고 하는데, 왜 θ를 최소화하는 것인지, 이 식으로 어떻게 θ가 최소화되는 것인지는 아직 잘 이해를 못했다. (영어라서 말을 잘 이해못한 것일 수도 있다..)
이제 비용함수 J(θ)를 구했으니 이것을 최소화시켜서 예측을 잘 하는 모델로 훈련을 해보자.
J(θ)를 최소화하기 위해 θ를 업데이트해야한다.
θ의 업데이트는 아래의 식과 같이 진행된다.

여기서 알파(α) 뒤의 식은 J(θ)의 도함수를 계산하는 식이라고 한다. 이 부분을 전개를 해주시면서 설명해주셨는데, 전개가 이해는 됐지만 다시 글로써 설명하기가 어려워서 전개부분은 건너 뛴다. 전개해보면 아래와 같은 식이 된다.
J(θ), 즉, 모델의 예측값과 실제 y값의 차이를 제곱한 것의 전개는 다음 영상을 참고하면 도움이 될 것이다.
다만, 다음 영상은 최소제곱법을 설명한 것으로, 비용함수와의 차이는 조금 있을 것이다.

여기서, α는 learning rate라고 하는데, 이 알파는 여러 가지 값(0.01, 0.1, 1, 10, 100 등)을 시도해보고 최적의 값을 선택할 수 있다.
Batch Gradient Descent & Stochastic Gradient Descent
Gradient Descent의 단점은 데이터가 너무 많을 경우, 매개변수(θ)를 한 번 업데이트하는데 1~m까지의 데이터에 대해
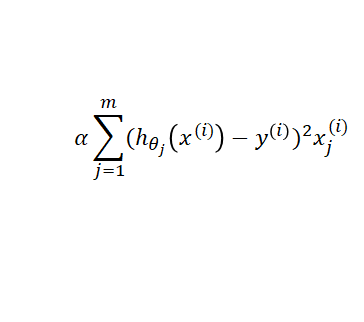
이 식을 계산을 해주어야한다. 즉, 컴퓨터 비용이 너무 많이 들고, 느리다.
이것을 바로 Batch Gradient Descent이다. 전체 데이터에 대해 계산하여 업데이트 하는 방식이다.
전체 데이터를 보고 계산한다는 장점이 있지만, 너무 느리다는 단점이 있어 이를 보완하기 위해 나온 것이
Stochastic Gradient Descent, SGD 이다.
SGD는 한 번에 1개의 데이터만 보고 θ를 업데이트 하는 방식이라고 생각하면된다.

왼쪽의 이미지처럼 SGD는 매우 많이 진동한다. 그리고 GD(Gradient Descent)처럼 수렴하지는 않는다.
그래서 SGD가 어느 정도 수렴한 뒤(진동의 폭이 작아진 뒤) 학습률 α를 줄여가며 최적의 파라미터(θ)를 찾는 것 방법을 많이 사용한다고 한다. (왜냐면 SGD는 시간이 지날 수록 global minima 근처에서 진동하니까.)
Dataset의 크기가 너무 클 경우, SGD를 사용하여 빠르게 구현할 수 있다.
Normal Equation
앞서 살펴보았던 Gradient Descent 방식은 조금씩 파라미터를 업데이트해가며 최적의 값을 얻는 방식이다. 그렇다면 한 번에 얻는 방법은 없을까?
이것이 바로 Normal Equation(정규방정식) 이다. 단, 정규방정식은 Linear Regression에서만 동작한다.
정규방정식을 유도하는 과정을 설명해주셨지만... ABC에서 갑자기 Z로 넘어간 느낌이라 제대로 이해하지는 못해서 정리를 하지 못하겠다..

위와 같은 내용이었는데, 대충 x가 벡터이면 f(x)를 미분하면 그 각각의 원소를 미분하면 되는 것이다. 그리고 2번 미분한 것의 미분 과정을 설명해주셨는데 아직 잘 모르겠다..

유도과정이후 위와 같은 식이 나오게 되고, 이 식을 다시 정리해서 θ를 구하면 아래와 같다.

아는 내용이라고 생각했는데 수학적인 내용도 많이 나오고, 영어로 진행되고.. 다시 블로그에 정리하다보니 많이 몰랐다는 것을 알게되었다. 패스트캠퍼스 강의로 딥러닝 수학도 끊어놨는데 수학 정말 열심히 해야겠다...
'인공지능' 카테고리의 다른 글
| DeepLearning - Ian Goodfellow 읽기 시작! (0) | 2022.03.11 |
|---|---|
| [CS229-Autumn 2018] Lecture 1 - Welcome (0) | 2021.08.25 |